Ansys Fluent Day 1, Intro
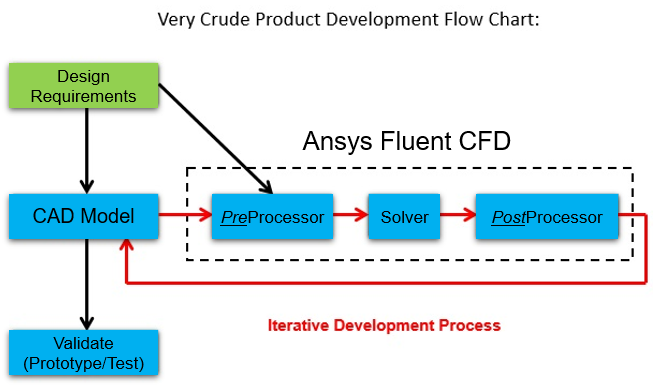
Overview: CFD workflow:
+ CFD (in general): + Ansys:
– Pre-processor – CAD Prep, Meshing, and Setup
– Solver – Solve/Converge
– Post processor – Review Results

(Re)Introduction to Fluids:
- A Fluid is: a substance with no fixed shape that deforms easily under external forces.
- Examples: Liquids and Gases
- Two most common fluids: Air & Water

(Re)Introduction to Fluids:
- Fluid Properties:
- Density, rho = Mass/Volume
- Viscosity, mu = Resistance to deformation (as a result of shear stress). Commonly called the “thickness” of a fluid.

(Re)Introduction to Fluids:
- Most fluids have a constant Viscosity, and are thus called a “Newtonian Fluid”.
- Special case #1 = Non-Newtonian Fluid: Variable Viscosity, usually as a function of the shear rate (speed with which the fluid is being moved)
- “Shear Thinning”
- Blood
- Ketchup
- “Non Drip Paint”
- “Shear Thinning”
- “Shear Thickening”
- Oobleck

(Re)Introduction to Fluids:
- Flow Characteristics:
- Velocity, V = Distance/Time
- Flow Regimes:
- Subsonic: < 650 mph
- Transonic: 650 – 767 mph
- Supersonic: 767 – 4,000 mph
- Hypersonic: >4,000 mph
(Re)Introduction to Fluids:
- Speed of Sound = ~767 mph (M=1.0)
- When M>1.0, the air is rapidly compressed (increase in pressure, temperature and density)
- Special case #2 = Compressible Flow: Where fluids (mostly gasses) which exhibit significant changes in density.

(Re)Introduction to Fluids:
- Special case #3 = Inviscid: The viscous forces within the flow are negligible. This can be true for fluid of non-zero viscosity! (e.g. High speed, high atmospheric flow away from a wall).

(Re)Introduction to Fluids:
- Fluid-Flow Characteristics:
- Reynold’s Number, Re: The ratio of Inertial Forces to Viscous Forces
- Low Re – Laminar
- High Re – Turbulent
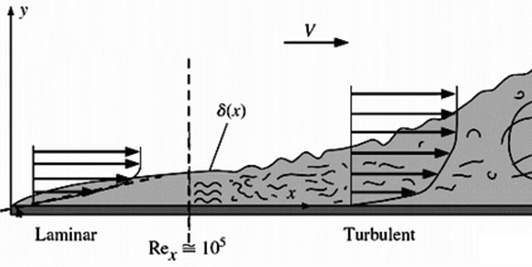
(Re)Introduction to Fluids:
- Boundary Layer
- Region of fluid flow near a wall, where velocity transitions from 0 to V
- Region where viscous forces dominate the flow!
- Critical Reynolds Number, Rex: Where Laminar flow transitions to Turbulent
- Internal Flow: For Flow through a Pipe, Rex = 2300
- External Flow: For Flow over a Plate, Rex = 5x10E5
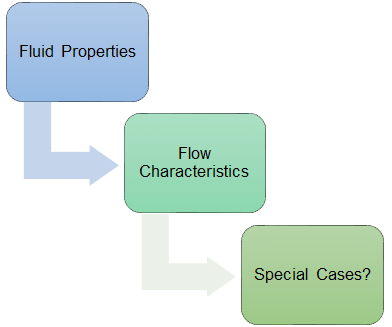
Pre-CFD Checklist:
- What are the fluid properties?
- Density, Viscosity
- What are the flow characteristics?
- Velocity, Reynold’s Number at entrance, where are there Boundary Layers/Walls?
- Do any special cases apply?
- Non-Newtonian?
- Compressible?
- Inviscid?
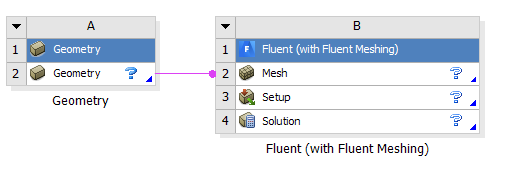
Start:
- Open Workbench
- Drag/Drop a Geometry Component
- Drag/Drop Fluent (with Fluent Meshing)
- Save the Workbench File

Start:
- Launch SpaceClaim from Workbench
- Import the Nozzle/Diffuser file here: nozzle_diff.x_t

Prepare:
- Use SpaceClaim to prepare the geometry for meshing
- Cut into a "quarter symmetry" model
- Establish Names Selections
- Inlet (Larger Diameter)
- Outlet (Smaller Diameter)
- Symmetry Planes
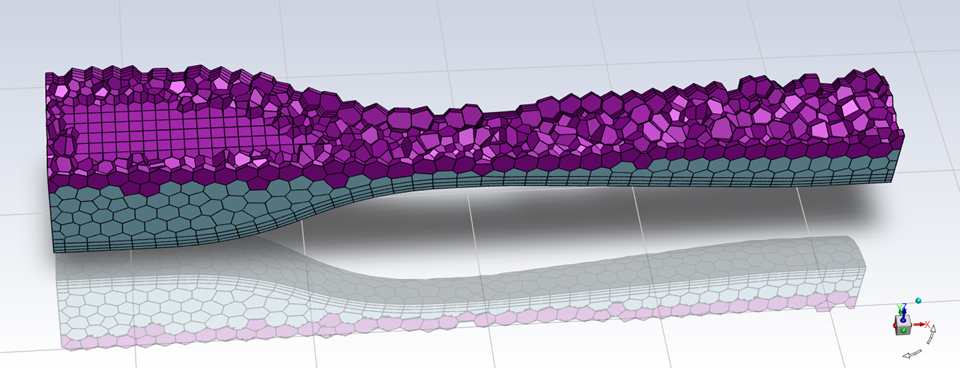
Mesh:
- Import into the Watertight Workflow
- Create a volume mesh using the default mesh sizes
Best Practice:
- Check units in Workbench beforehand

Setup:
- After familiarizing yourself with the interface, audit the model for accuracy
- Physics Models & Materials
- Boundary Conditions
- Set Inlet to 12.5 m/s
Best Practice:
- Check mesh upon entry

Solve the Analysis:
- Set to Laminar & Solve 50 Iterations
- Observe Convergence
- Post Process
- Create a Velocity Contour
- Create Mesh Display
- Create Scene with Velocity & Mesh

Post Process:
- Use various Post Processing Tools:
- Vectors
- Pathlines
- Particle Tracks
- Iso Surfaces
- Create your Favorite Scene
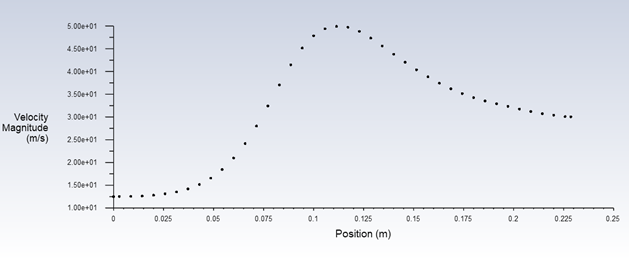
Double Check Your Work:
- How do we know we have the right answer?
- We compare it to “The Math”
- What velocity should we have at the narrow section? The exit?
- Create Reports
- Inlet Flow Rate & Outlet Flow Rate
- Create Plot along pipe Centerline

File Management:
- Don't forget to save often!
- Discuss the different files types
- Mesh
- Case
- Data

Introduction to CFD Mathematics
- Infinitesimal Fluid Element (Control Volume)
- This volume has both Fluid Properties and Flow Characteristics at a certain point in time
- Density
- Viscosity
- Pressure
- Velocity
- Temperature
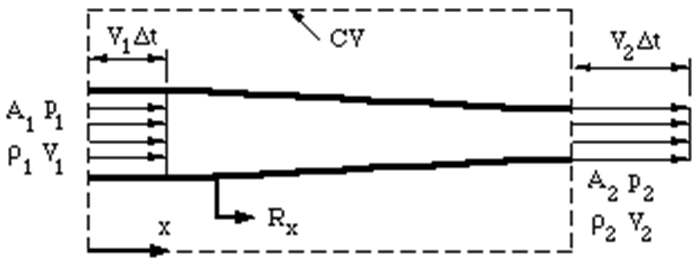
Introduction to CFD Mathematics
- Assume the fluid is represented by a “Control Volume”
- Bernoulli says: P + ½*rho*V^2 + rho*g*h = constant
- Pressure, density, Velocity, Gravity, Height
- Additionally:
- A1V1 = A2V2 & P1 – P2 = ½*rho (V2^2 – V1^2)
- So, as Area goes down, Velocity goes up (linearly)
- And as Velocity goes up, Pressure goes down (quadratically)

Modeling Turbulent Flow
- Should we include turbulence?
- Calculate Inlet Re (recall: Turb>2,300+)
- Let’s add turbulence, and solve 100 more iterations
- Why are we able to just continue at the last iteration, even though the entire physics have changed?
- Why did the analysis stop early?
More CFD Mathematics:
- Governing Equations conserve Mass, Momentum, (sometimes) Energy
- These equations must be solved...
- at every iteration
- for every element

More CFD Mathematics:
- Velocity, Mass, Force, and Temperature, are all COUPLED. Thus, the need for an iterative approach.
- We sum this all up to a set of equations called the “Navier Stokes equations (shown here, broken down to the 3 directions (u,v,w), which are velocities in (x, y, z):

Residuals:
- Residuals are the leftover values from each iteration (in the real world, they are zero)
- This is not computationally feasible
- Rule of Thumb:
- Default = .001 (1E-03) – This is for a quick answer.
- Tighter = .0001 (1E-04) – This is for a more accurate answer.
- Fine = .00001 (1E-05) – This is for a solution that you can start to trust.
- Extra Fine = .000001 (1E-06) – This is for an answer that you plan to publish and/or utilize academically.

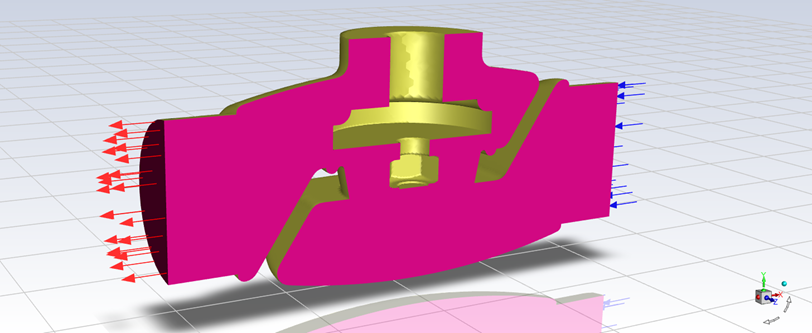
Globe Valve:
- Import, Extract Water Volume, Cut in Half
- Suppress Structure for Physics
- Named Selections: Inlet, Outlet, Symmetry
Download here: globe_valve7_x_t

Mesh:
- Create a Poly-Hex Core Mesh using the Fluent Watertight Workflow
Setup:
- Fluid = Water
- Inlet = 0.002 meter/sec
- Is it turbulent?
- Set Residuals to 1e-4, and solve 100 iterations

Assess for Accuracy & Quality:
- How can we trust the results?
- Check the velocity at the exit, or at any other location – Compare to Bernoulli's equation
- Check for mesh independence!
- Add a mesh control, and re-solve
- Surface Control
- Gap Elements

Tell the Right Story, and Optimize the Design:
- Create a scene showing the pressure drop and velocity streamlines on the symmetry plane
- Make a design change to minimize the pressure drop in the flow
© Fastway Engineering. All Rights Reserved. May not be duplicated without express written consent.